[PR]
2026年03月12日
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
スラロームによる移動距離近似、その4
2017年04月18日
第4回です。
これまでの記事は1回目の目次からどうぞ。
今回はクロソイドの移動距離を近似を用いて求めていきます。
タイトル回収ですね。
まずクロソイドについておさらいから始めていきましょう。
クロソイド曲線とは高速道路のインターチェンジで使われるような曲線です。
詳しい説明についてはこちらの方に譲らせていただきます。
スラロームにおけるクロソイド曲線について考えてみましょう。
このクロソイド曲線は、角加速区間および角減速部分に出てきます。
その移動距離は解析的には計算できないわけですが、数式で表せないというわけではありません。
重心速度vでスラローム中のマウスは以下のような図で模式的に表せます。
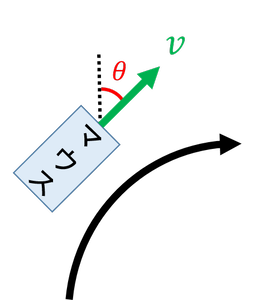
ここでθは機体の角度を表し、時間に依存した変数です。
移動距離を考えると以下のようになります。

先ほどの式(6)が解けないことが、スラロームの移動距離がわからない原因です。
Mice内で一般的(?)な手法では、数値解析により解決していました。
本記事ではマクローリン展開により解決します。
具体的には、非積分関数をマクローリン展開したうえで積分します。
また今回の手法はこのサイトを非常に参考にしております。
スラロームにおけるクロソイドでは角度の小さい部分を用いるため、時刻 t が0近傍であると仮定してマクローリン展開します。

x軸方向の移動距離は以上のように表せます。
しかし、今回はパラメータとして時間でなく角度を用いたいので、機体の角速度をωと置いて、式(8)を変形していきます。

これで、クロソイドのx軸方向の移動距離を表すことができました。
同様にy軸方向についても行っていきます。

よって、クロソイドの移動距離を表すことができました。
マクローリン展開を用いることでクロソイドの移動距離を求めることができました。

円弧のときと同様に、移動距離が曲率半径Rとパラメータ(加速角度θA)による関数の積で表されています。
そのため、どうやら移動距離とパラメータより曲率半径を求めることができそうです。
次回はスラローム全体の移動距離をどう表せるのかという点について扱っていきます。
今回はまだ終わりません。おまけがあります。お得ですね。
ここでは、皆さんが気になっているであろうマクローリン展開の誤差について考えていきます。
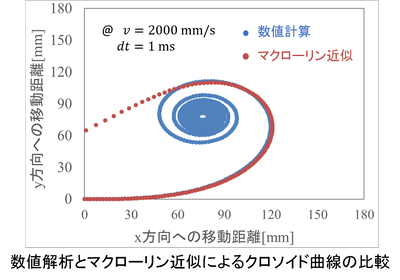
上図はクロソイド曲線について、Excelで数値計算した軌跡とマクローリン近似による軌跡を比較したものです。
重心速度を2000mm/s、微小時間を1msとして計算しています。
高速ターンにおいてスリップ角を考慮しないのは現実的ではありませんが、ここでは誤差の影響が顕著に出るようv=2000mm/sとしました。
この図を見ると見た目には、スラロームに用いる低角度領域ではよく近似できているように見えます。
しかし、図からはどれほどずれているかわかりません。
というわけで、両者の差をグラフにしたものが下図になります。
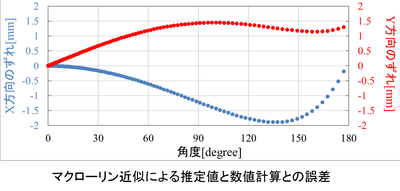
この図は、
角加速度515rad/ss
重心速度2000mm/s
のパラメータにおいて
「マクローリン近似による推定値」と
「微小時間を1msとして計算した数値計算」を比較したものです。
横軸は機体の角度、縦軸はそれぞれX方向とY方向における差を示しています。
これを見ると180度までの範囲で、ズレは最大でも2mm程度だとわかります。
スラロームとして考えると180度ターンのとき角度が最大なので、クロソイド曲線としては90度までとなります。
そのため、近似によるズレは最大でも1.5mm程度で済みそうです。
皆さんが如何ほどの精度で機体の制御を行っているかはわかりませんが、~2mm程度のズレであれば調整範囲内といってよいのではないでしょうか。
少なくとも私のマウスでは理論値と現実の軌跡とのズレは、これよりはるかに大きいため、調整によって丸めこめると考えています。
最後に重心速度を変えたときズレはどのように変化するかを載せて今回は締めさせていただきます。
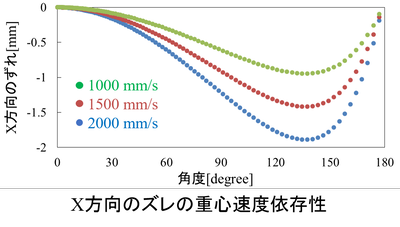
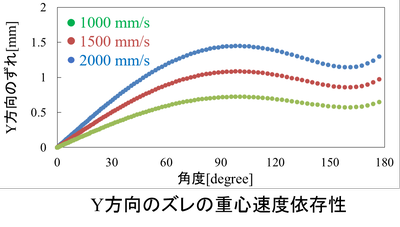
式(11)、(13)からも明らかなように速度が大きくなればズレも大きくなります。
これまでの記事は1回目の目次からどうぞ。
今回はクロソイドの移動距離を近似を用いて求めていきます。
タイトル回収ですね。
クロソイドの移動距離
クロソイドとは
まずクロソイドについておさらいから始めていきましょう。
クロソイド曲線とは高速道路のインターチェンジで使われるような曲線です。
詳しい説明についてはこちらの方に譲らせていただきます。
スラロームにおけるクロソイド曲線について考えてみましょう。
このクロソイド曲線は、角加速区間および角減速部分に出てきます。
その移動距離は解析的には計算できないわけですが、数式で表せないというわけではありません。
重心速度vでスラローム中のマウスは以下のような図で模式的に表せます。
ここでθは機体の角度を表し、時間に依存した変数です。
移動距離を考えると以下のようになります。
マクローリン近似
先ほどの式(6)が解けないことが、スラロームの移動距離がわからない原因です。
Mice内で一般的(?)な手法では、数値解析により解決していました。
本記事ではマクローリン展開により解決します。
具体的には、非積分関数をマクローリン展開したうえで積分します。
また今回の手法はこのサイトを非常に参考にしております。
スラロームにおけるクロソイドでは角度の小さい部分を用いるため、時刻 t が0近傍であると仮定してマクローリン展開します。
x軸方向の移動距離は以上のように表せます。
しかし、今回はパラメータとして時間でなく角度を用いたいので、機体の角速度をωと置いて、式(8)を変形していきます。
これで、クロソイドのx軸方向の移動距離を表すことができました。
同様にy軸方向についても行っていきます。
よって、クロソイドの移動距離を表すことができました。
まとめ
マクローリン展開を用いることでクロソイドの移動距離を求めることができました。
円弧のときと同様に、移動距離が曲率半径Rとパラメータ(加速角度θA)による関数の積で表されています。
そのため、どうやら移動距離とパラメータより曲率半径を求めることができそうです。
次回はスラローム全体の移動距離をどう表せるのかという点について扱っていきます。
マクローリン展開の誤差について
今回はまだ終わりません。おまけがあります。お得ですね。
ここでは、皆さんが気になっているであろうマクローリン展開の誤差について考えていきます。
上図はクロソイド曲線について、Excelで数値計算した軌跡とマクローリン近似による軌跡を比較したものです。
重心速度を2000mm/s、微小時間を1msとして計算しています。
高速ターンにおいてスリップ角を考慮しないのは現実的ではありませんが、ここでは誤差の影響が顕著に出るようv=2000mm/sとしました。
この図を見ると見た目には、スラロームに用いる低角度領域ではよく近似できているように見えます。
しかし、図からはどれほどずれているかわかりません。
というわけで、両者の差をグラフにしたものが下図になります。
この図は、
角加速度515rad/ss
重心速度2000mm/s
のパラメータにおいて
「マクローリン近似による推定値」と
「微小時間を1msとして計算した数値計算」を比較したものです。
横軸は機体の角度、縦軸はそれぞれX方向とY方向における差を示しています。
これを見ると180度までの範囲で、ズレは最大でも2mm程度だとわかります。
スラロームとして考えると180度ターンのとき角度が最大なので、クロソイド曲線としては90度までとなります。
そのため、近似によるズレは最大でも1.5mm程度で済みそうです。
皆さんが如何ほどの精度で機体の制御を行っているかはわかりませんが、~2mm程度のズレであれば調整範囲内といってよいのではないでしょうか。
少なくとも私のマウスでは理論値と現実の軌跡とのズレは、これよりはるかに大きいため、調整によって丸めこめると考えています。
最後に重心速度を変えたときズレはどのように変化するかを載せて今回は締めさせていただきます。
式(11)、(13)からも明らかなように速度が大きくなればズレも大きくなります。
PR
スラロームによる移動距離近似、その3
2017年04月14日
ようやく3回目です。
まだイントロが終わった段階でしかありませんが。
これまでの記事は1回目の目次からどうぞ。
というわけで数式をいじりながら移動距離を求めていきます。
全部やると長くなりそうなので、今回は円弧部分を求めるところまで。
計算に移る前に以降使う文字の定義を決めておきましょう。
前回の記事からスラロームパラメータとは、「角加速度、目標角度、加速角度、重心速度」だとわかりました。これらをそれぞれ以下のように置くことにします。

また、機体の角度をθと置くことにします(下図参照)。

すると、スラロームの各要素は、それぞれθが以下の範囲内であると表せます。

※ここでは、角減速は角加速と同じように行うとする。つまり、角加速度の絶対値が同じであり、かつ角減速し角速度0になるまでに必要な角度は加速角度θAと等しい。
まず、簡単な円弧部分の移動距離について求めていきます。
スラロームから円弧部分のみを取り出したのが下図になります。

ここで、円弧の曲率半径をRと置きました。
また、移動距離を考えるので、座標軸としてx軸y軸を追加し円の中心をその原点とします。
θAとθT-θAが何故このように決まるのかわからない人は接線をひいて考えることで理解の助けとなるかもしれません。
さて、では円弧の移動距離を考えていきます。

よって、円弧のx軸方向とy軸方向への移動距離をそれぞれ求めることができました。
式(3)、式(4)からパラメータと移動距離の関係を知ることができます。
また、式(3)、式(4)は円弧を決める変数Rと人間が決めるパラメータθTθAによる関数の積の形で移動距離を表すことができています。
よって、将来的には、移動距離とパラメータから曲率半径を求める(円弧の軌跡を求める)ことができそうだと予想されます。
とはいえ、それができるかはクロソイドがどう表されるかによりますが。
というわけで、今回はここまで。
今回わかったことは円弧の移動距離は以下のように表されます。
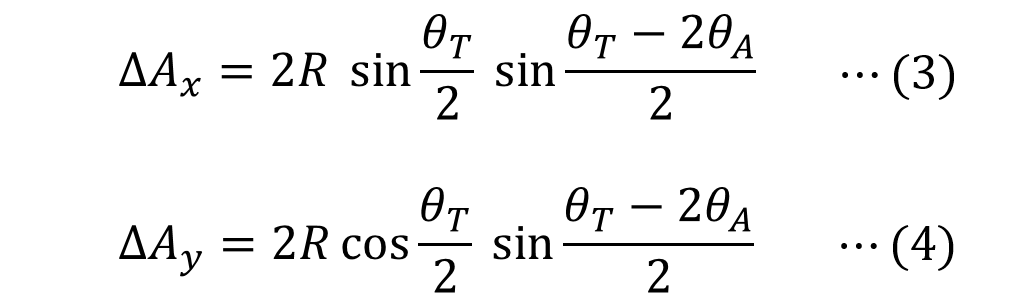
次回はついにクロソイドに入りたいと思います。
まだイントロが終わった段階でしかありませんが。
これまでの記事は1回目の目次からどうぞ。
というわけで数式をいじりながら移動距離を求めていきます。
全部やると長くなりそうなので、今回は円弧部分を求めるところまで。
文字の定義
計算に移る前に以降使う文字の定義を決めておきましょう。
前回の記事からスラロームパラメータとは、「角加速度、目標角度、加速角度、重心速度」だとわかりました。これらをそれぞれ以下のように置くことにします。
また、機体の角度をθと置くことにします(下図参照)。
すると、スラロームの各要素は、それぞれθが以下の範囲内であると表せます。
※ここでは、角減速は角加速と同じように行うとする。つまり、角加速度の絶対値が同じであり、かつ角減速し角速度0になるまでに必要な角度は加速角度θAと等しい。
円弧の移動距離
まず、簡単な円弧部分の移動距離について求めていきます。
スラロームから円弧部分のみを取り出したのが下図になります。
ここで、円弧の曲率半径をRと置きました。
また、移動距離を考えるので、座標軸としてx軸y軸を追加し円の中心をその原点とします。
θAとθT-θAが何故このように決まるのかわからない人は接線をひいて考えることで理解の助けとなるかもしれません。
さて、では円弧の移動距離を考えていきます。
よって、円弧のx軸方向とy軸方向への移動距離をそれぞれ求めることができました。
式(3)、式(4)からパラメータと移動距離の関係を知ることができます。
また、式(3)、式(4)は円弧を決める変数Rと人間が決めるパラメータθTθAによる関数の積の形で移動距離を表すことができています。
よって、将来的には、移動距離とパラメータから曲率半径を求める(円弧の軌跡を求める)ことができそうだと予想されます。
とはいえ、それができるかはクロソイドがどう表されるかによりますが。
まとめ
というわけで、今回はここまで。
今回わかったことは円弧の移動距離は以下のように表されます。
次回はついにクロソイドに入りたいと思います。
スラロームによる移動距離近似、その2
2017年04月13日
第2回です。第1回(導入)はこちら。
今回は具体的な数式とかをいじる前に何を求めればよいかとかを整理したいと思います。
実質的に導入その2。
具体的に近似計算とかの話に移る前に、まずはスラロームについておさらいしておきましょう。
基本的には

スラロームとは先ほどの図のような軌跡を描くカーブのことです。
では、私たちがこの軌跡において最も重視しているものは何でしょうか?
それはスラロームによる移動量のはずです。
つまり、スラロームが終わった後に、どの位置にいるかということです。
(壁や柱にぶつからない軌跡を通ることも大事ですが、始点位置と終点位置が合っていれば無茶な軌跡を通ることはないとします。[要出展])
ここで、移動距離の観点で考え、先ほどの図を少し変更しましょう。
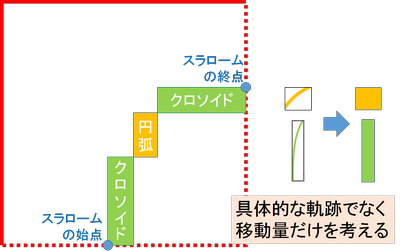
この図より、クロソイドと円弧のそれぞれの縦横方向の移動距離(それぞれの長方形の縦横の長さ)がわかれば、スラローム全体で移動する距離を表すことができそうです。
つまり、これらとスラロームパラメータとの対応を求めれば、始点と終点を決めればスラロームパラメータを決めることができます。
具体的に移動距離を求める前に、スラロームに必要なパラメータについて考えておきましょう。
スラロームをするためには、角速度が以下の図のように変化する必要がありました。
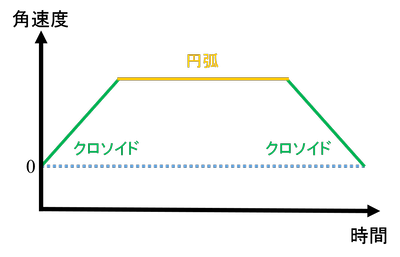
このグラフを描くために必要な情報が、スラロームを行うために必要なパラメータになります。
それを図中に書き入れたものが下図になります。
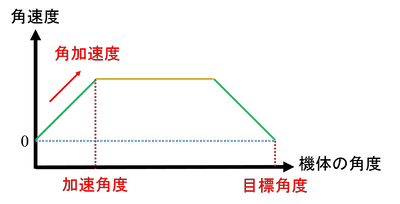
※この図では、パラメータとしての取り扱いの関係から横軸を時間から機体の角度に変更しています。
図中に赤字で示した
目標角度(何度のターンをするのか)
加速角度(何度まで角加速するのか)
角加速度
がわかれば、図のような台形加速を行うことが可能なはずです。(最大角速度は角加速度と加速角度より求めることができるので、パラメータとしては選択しないことにします。)
そして、これらに機体の重心速度を加えたものがスラロームに必要なパラメータとなります。
※前距離、後距離と呼ばれるスラローム前後のオフセットについては連載後半で触れます。
やりたいこと
「始点と終点の位置からスラロームパラメータを求める」
そのために必要なこと
「円弧とクロソイドによる移動距離が、スラロームパラメータによってどのように表されるか知る」
スラロームパラメータって?
「目標角度、加速角度、角加速度、重心速度」
次回は移動距離を求めていきます。ついに数式が登場!…のはず。
今回は具体的な数式とかをいじる前に何を求めればよいかとかを整理したいと思います。
実質的に導入その2。
パラメータを決めるために必要なもの
スラロームについてのおさらい
具体的に近似計算とかの話に移る前に、まずはスラロームについておさらいしておきましょう。
基本的には
クロソイド曲線 ⇒ 円弧 ⇒ クロソイド曲線
でした。
忘れてる方やそもそもスラローム知らないとかいう人は、昔書いた記事読んでください(宣伝)。スラロームの軌跡の中で重要な要素
スラロームとは先ほどの図のような軌跡を描くカーブのことです。
では、私たちがこの軌跡において最も重視しているものは何でしょうか?
それはスラロームによる移動量のはずです。
つまり、スラロームが終わった後に、どの位置にいるかということです。
(壁や柱にぶつからない軌跡を通ることも大事ですが、始点位置と終点位置が合っていれば無茶な軌跡を通ることはないとします。[要出展])
ここで、移動距離の観点で考え、先ほどの図を少し変更しましょう。
この図より、クロソイドと円弧のそれぞれの縦横方向の移動距離(それぞれの長方形の縦横の長さ)がわかれば、スラローム全体で移動する距離を表すことができそうです。
つまり、これらとスラロームパラメータとの対応を求めれば、始点と終点を決めればスラロームパラメータを決めることができます。
スラロームに必要なパラメータは?
具体的に移動距離を求める前に、スラロームに必要なパラメータについて考えておきましょう。
スラロームをするためには、角速度が以下の図のように変化する必要がありました。
このグラフを描くために必要な情報が、スラロームを行うために必要なパラメータになります。
それを図中に書き入れたものが下図になります。
※この図では、パラメータとしての取り扱いの関係から横軸を時間から機体の角度に変更しています。
図中に赤字で示した
目標角度(何度のターンをするのか)
加速角度(何度まで角加速するのか)
角加速度
がわかれば、図のような台形加速を行うことが可能なはずです。(最大角速度は角加速度と加速角度より求めることができるので、パラメータとしては選択しないことにします。)
そして、これらに機体の重心速度を加えたものがスラロームに必要なパラメータとなります。
※前距離、後距離と呼ばれるスラローム前後のオフセットについては連載後半で触れます。
まとめ
やりたいこと
「始点と終点の位置からスラロームパラメータを求める」
そのために必要なこと
「円弧とクロソイドによる移動距離が、スラロームパラメータによってどのように表されるか知る」
スラロームパラメータって?
「目標角度、加速角度、角加速度、重心速度」
次回は移動距離を求めていきます。ついに数式が登場!…のはず。
スラロームによる移動距離近似、その1
2017年04月12日
こんにちは、
マウスに触れなくなって久しいのでリハビリを兼ねてこの記事を書くことにします。
内容は、近似を用いてスラロームによる移動距離を見積もることについてです。
結構長くなりそうなので、連載記事にするつもり。失踪せずに書き上げたい…!
また、前提として、積分とか微分とかマクローリン展開とかの数学の知識を必要とするのでご了承ください。
目次
一連の連載記事の目次にしたい
導入
※本記事では、単純な クロソイド⇒円弧⇒クロソイド のスラロームを考えています。
タイトルにもなっているスラローム走行について考える。
スラローム走行をマイクロマウスで実装するには様々なパラメータを決める必要がある。
例えば、角加速度であったり、最大角速度であったりといったもの。
今回は、スラローム実装についての詳しい話をするつもりはないので、気になる人は各自このへんから調べてほしい。
話をもどして。
しかしながら、こういったパラメータを決めるのは、なかなか難しい。
何故なら、スラローム走行をする際に、私たちは望む軌跡を通ってほしいが、これらのパラメータとの対応関係がわからないからだ。
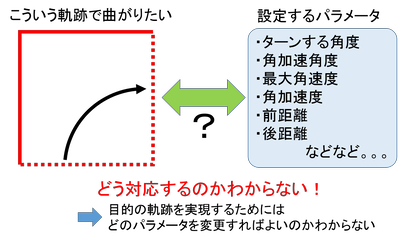
どうして対応関係がわからないのか、という理由はスラロームを行うために必要なクロソイド曲線と呼ばれる部分が解析的に解けないことに起因している。
が、その辺の話は主題から少しずれるので、美少女のブログを参考にしてほしい。
ここで覚えておいてほしいのは、軌跡からパラメータを推定するのは難しい。
その理由は、数式はわかるけど積分が解析的に解けないから。
スラロームをしているということは、何かしらの方法でパラメータを決めているわけで。
じゃあどうやっているのか?
自分の知る限り、Miceでは二通りの方法がある。
・別途シュミレータを作り、パラメータに対応する軌跡を数値計算で求め、それを確認しながらパラメータを探す
・マイコン内で、パラメータを少しづつかえ、ループをまわし、数値計算により軌跡の移動量を求め、パラメータを決める
これらの方法は、マウスの中で行うか外で行うかの違いだけで、本質的にはどちらも同じことをしている。と思う。
つまり、解析的に解けない積分を数値計算することで軌跡を推定し、そのパラメータ毎に推定した軌跡の中から求めるものを選択する、ということを行っている。
この方法なら、数値計算による微小な誤差はあるものの、求める軌跡を描くパラメータを求めることができる。
しかし、ループを回すためパラメータ推定にはある程度の時間がかかり、実質的に走行前に臨む軌跡のパラメータを決め打ちすることとなる。
例えば、走行中に壁によってるから小回りの軌跡でターンしようとかは難しい。
あとシュミレータだとパラメータ振るのがめんどい。。。
上で紹介した方法では、スラロームパラメータ同定が困難であるという問題を
解析的に解けないから数値計算する
といった方法で解決していた。
そこで、本記事では
数値計算ではなく近似解を用いる
ことを提案する。
近似解を用いて、マウスで動かすのに妥当な範囲で、数式でパラメータと軌跡の対応がわかれば求める軌跡から簡単にパラメータを決めることができる。かもしれない。
近似計算といっても美少女が紹介している研究レベルの難しい近似ではなく、マクローリン近似で行う。
というか、やってみたら意外とうまくいきそうなので紹介しますというのが本音。
次回は、スラロームをするためには何を求める必要があるのか考えていきたい。
マウスに触れなくなって久しいのでリハビリを兼ねてこの記事を書くことにします。
内容は、近似を用いてスラロームによる移動距離を見積もることについてです。
結構長くなりそうなので、連載記事にするつもり。失踪せずに書き上げたい…!
また、前提として、積分とか微分とかマクローリン展開とかの数学の知識を必要とするのでご了承ください。
目次
一連の連載記事の目次にしたい- 導入(この記事)
- 移動距離推定には何が必要か(導入その2)
- 円弧部分の移動距離について
- クロソイド部分の移動距離について
- スラローム全体の移動距離について
- 残る問題点とその解決法(予定)
- まとめ(予定)
導入
スラロームのパラメータを決めるのって難しいよね?
※本記事では、単純な クロソイド⇒円弧⇒クロソイド のスラロームを考えています。
タイトルにもなっているスラローム走行について考える。
スラローム走行をマイクロマウスで実装するには様々なパラメータを決める必要がある。
例えば、角加速度であったり、最大角速度であったりといったもの。
今回は、スラローム実装についての詳しい話をするつもりはないので、気になる人は各自このへんから調べてほしい。
話をもどして。
しかしながら、こういったパラメータを決めるのは、なかなか難しい。
何故なら、スラローム走行をする際に、私たちは望む軌跡を通ってほしいが、これらのパラメータとの対応関係がわからないからだ。
どうして対応関係がわからないのか、という理由はスラロームを行うために必要なクロソイド曲線と呼ばれる部分が解析的に解けないことに起因している。
が、その辺の話は主題から少しずれるので、美少女のブログを参考にしてほしい。
ここで覚えておいてほしいのは、軌跡からパラメータを推定するのは難しい。
その理由は、数式はわかるけど積分が解析的に解けないから。
じゃあ皆はどうやってパラメータを決めてるの?
とはいえ、皆は平然とスラロームしているわけで。スラロームをしているということは、何かしらの方法でパラメータを決めているわけで。
じゃあどうやっているのか?
自分の知る限り、Miceでは二通りの方法がある。
・別途シュミレータを作り、パラメータに対応する軌跡を数値計算で求め、それを確認しながらパラメータを探す
・マイコン内で、パラメータを少しづつかえ、ループをまわし、数値計算により軌跡の移動量を求め、パラメータを決める
これらの方法は、マウスの中で行うか外で行うかの違いだけで、本質的にはどちらも同じことをしている。と思う。
つまり、解析的に解けない積分を数値計算することで軌跡を推定し、そのパラメータ毎に推定した軌跡の中から求めるものを選択する、ということを行っている。
この方法なら、数値計算による微小な誤差はあるものの、求める軌跡を描くパラメータを求めることができる。
しかし、ループを回すためパラメータ推定にはある程度の時間がかかり、実質的に走行前に臨む軌跡のパラメータを決め打ちすることとなる。
例えば、走行中に壁によってるから小回りの軌跡でターンしようとかは難しい。
あとシュミレータだとパラメータ振るのがめんどい。。。
この記事の目的
では、この記事では何をするのか?という点である。上で紹介した方法では、スラロームパラメータ同定が困難であるという問題を
解析的に解けないから数値計算する
といった方法で解決していた。
そこで、本記事では
数値計算ではなく近似解を用いる
ことを提案する。
近似解を用いて、マウスで動かすのに妥当な範囲で、数式でパラメータと軌跡の対応がわかれば求める軌跡から簡単にパラメータを決めることができる。かもしれない。
近似計算といっても美少女が紹介している研究レベルの難しい近似ではなく、マクローリン近似で行う。
というか、やってみたら意外とうまくいきそうなので紹介しますというのが本音。
次回は、スラロームをするためには何を求める必要があるのか考えていきたい。
全日本大会で探索ができなかった話
2016年11月22日
こんにちは
久しぶりの更新になります。
全日本マイクロマウス大会の感想でも書きます。
まずは、選手の皆さま、並びに運営を担当したスタッフの皆さまお疲れさまでした。
おかげさまで、とても楽しい大会でした。
マウスパーティや技術交流会では、去年一昨年以上にいろいろな人とおしゃべりでき、(Twitter)上での知り合いもたくさん増えました。
この調子でもっと友達を増やしていきたい。
Miceとしては後輩も同期も先輩も受賞し、益々勢いを増している感じでしたね。
Miceの一員として鼻が高いです。
で、僕はというとハーフエキスパートに出場しました。
鯉住です。
肝心の結果ですが、
第1走 R
第2走 R
第3走 R
第4走 R
第5走 R
はい、死亡です。
探索すらできませんでした。
Miceの一員として肩身が狭いです。。。
一応、備忘録代わりに、もうちょっと詳しく残しておきます。
どうやらセンサ値がよろしくなかったらしく、安定するための前壁制御で発信するという体たらく。
一応小細工として、その場でLEDとセンサの向きをずらしてみましたが、やはりダメ。
壁キレを読み間違えて(6,7)をゴールと認識して帰ってきてしまいました。
完全な調整不足ですね。
とはいえ、去年よりは探索できてるので、来年こそは最短できると信じて頑張りたいです。
まずは電通大のプチ大会で鯉住をびゅんびゅんさせてあげたいところです。
皆さん1年間お疲れさまでした。
また来年お会いしましょう。
