[PR]
2026年03月13日
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
スラロームによる移動距離近似、その4
2017年04月18日
第4回です。
これまでの記事は1回目の目次からどうぞ。
今回はクロソイドの移動距離を近似を用いて求めていきます。
タイトル回収ですね。
まずクロソイドについておさらいから始めていきましょう。
クロソイド曲線とは高速道路のインターチェンジで使われるような曲線です。
詳しい説明についてはこちらの方に譲らせていただきます。
スラロームにおけるクロソイド曲線について考えてみましょう。
このクロソイド曲線は、角加速区間および角減速部分に出てきます。
その移動距離は解析的には計算できないわけですが、数式で表せないというわけではありません。
重心速度vでスラローム中のマウスは以下のような図で模式的に表せます。
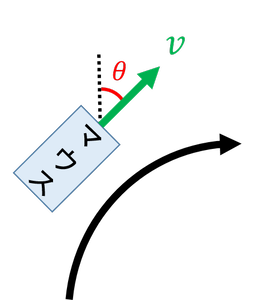
ここでθは機体の角度を表し、時間に依存した変数です。
移動距離を考えると以下のようになります。

先ほどの式(6)が解けないことが、スラロームの移動距離がわからない原因です。
Mice内で一般的(?)な手法では、数値解析により解決していました。
本記事ではマクローリン展開により解決します。
具体的には、非積分関数をマクローリン展開したうえで積分します。
また今回の手法はこのサイトを非常に参考にしております。
スラロームにおけるクロソイドでは角度の小さい部分を用いるため、時刻 t が0近傍であると仮定してマクローリン展開します。

x軸方向の移動距離は以上のように表せます。
しかし、今回はパラメータとして時間でなく角度を用いたいので、機体の角速度をωと置いて、式(8)を変形していきます。

これで、クロソイドのx軸方向の移動距離を表すことができました。
同様にy軸方向についても行っていきます。

よって、クロソイドの移動距離を表すことができました。
マクローリン展開を用いることでクロソイドの移動距離を求めることができました。

円弧のときと同様に、移動距離が曲率半径Rとパラメータ(加速角度θA)による関数の積で表されています。
そのため、どうやら移動距離とパラメータより曲率半径を求めることができそうです。
次回はスラローム全体の移動距離をどう表せるのかという点について扱っていきます。
今回はまだ終わりません。おまけがあります。お得ですね。
ここでは、皆さんが気になっているであろうマクローリン展開の誤差について考えていきます。
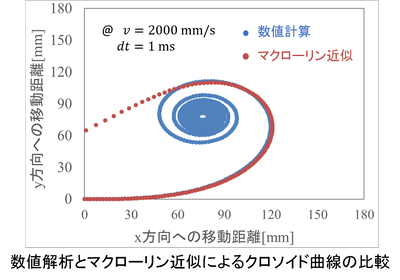
上図はクロソイド曲線について、Excelで数値計算した軌跡とマクローリン近似による軌跡を比較したものです。
重心速度を2000mm/s、微小時間を1msとして計算しています。
高速ターンにおいてスリップ角を考慮しないのは現実的ではありませんが、ここでは誤差の影響が顕著に出るようv=2000mm/sとしました。
この図を見ると見た目には、スラロームに用いる低角度領域ではよく近似できているように見えます。
しかし、図からはどれほどずれているかわかりません。
というわけで、両者の差をグラフにしたものが下図になります。
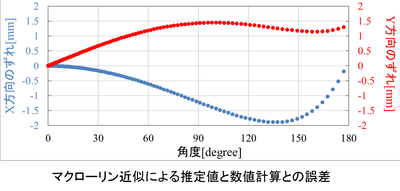
この図は、
角加速度515rad/ss
重心速度2000mm/s
のパラメータにおいて
「マクローリン近似による推定値」と
「微小時間を1msとして計算した数値計算」を比較したものです。
横軸は機体の角度、縦軸はそれぞれX方向とY方向における差を示しています。
これを見ると180度までの範囲で、ズレは最大でも2mm程度だとわかります。
スラロームとして考えると180度ターンのとき角度が最大なので、クロソイド曲線としては90度までとなります。
そのため、近似によるズレは最大でも1.5mm程度で済みそうです。
皆さんが如何ほどの精度で機体の制御を行っているかはわかりませんが、~2mm程度のズレであれば調整範囲内といってよいのではないでしょうか。
少なくとも私のマウスでは理論値と現実の軌跡とのズレは、これよりはるかに大きいため、調整によって丸めこめると考えています。
最後に重心速度を変えたときズレはどのように変化するかを載せて今回は締めさせていただきます。
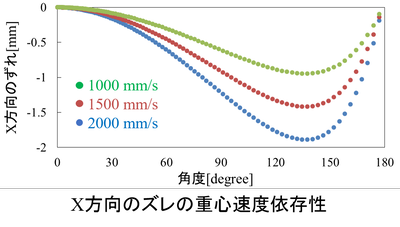
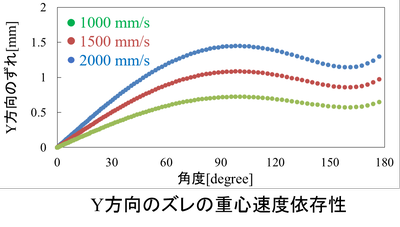
式(11)、(13)からも明らかなように速度が大きくなればズレも大きくなります。
これまでの記事は1回目の目次からどうぞ。
今回はクロソイドの移動距離を近似を用いて求めていきます。
タイトル回収ですね。
クロソイドの移動距離
クロソイドとは
まずクロソイドについておさらいから始めていきましょう。
クロソイド曲線とは高速道路のインターチェンジで使われるような曲線です。
詳しい説明についてはこちらの方に譲らせていただきます。
スラロームにおけるクロソイド曲線について考えてみましょう。
このクロソイド曲線は、角加速区間および角減速部分に出てきます。
その移動距離は解析的には計算できないわけですが、数式で表せないというわけではありません。
重心速度vでスラローム中のマウスは以下のような図で模式的に表せます。
ここでθは機体の角度を表し、時間に依存した変数です。
移動距離を考えると以下のようになります。
マクローリン近似
先ほどの式(6)が解けないことが、スラロームの移動距離がわからない原因です。
Mice内で一般的(?)な手法では、数値解析により解決していました。
本記事ではマクローリン展開により解決します。
具体的には、非積分関数をマクローリン展開したうえで積分します。
また今回の手法はこのサイトを非常に参考にしております。
スラロームにおけるクロソイドでは角度の小さい部分を用いるため、時刻 t が0近傍であると仮定してマクローリン展開します。
x軸方向の移動距離は以上のように表せます。
しかし、今回はパラメータとして時間でなく角度を用いたいので、機体の角速度をωと置いて、式(8)を変形していきます。
これで、クロソイドのx軸方向の移動距離を表すことができました。
同様にy軸方向についても行っていきます。
よって、クロソイドの移動距離を表すことができました。
まとめ
マクローリン展開を用いることでクロソイドの移動距離を求めることができました。
円弧のときと同様に、移動距離が曲率半径Rとパラメータ(加速角度θA)による関数の積で表されています。
そのため、どうやら移動距離とパラメータより曲率半径を求めることができそうです。
次回はスラローム全体の移動距離をどう表せるのかという点について扱っていきます。
マクローリン展開の誤差について
今回はまだ終わりません。おまけがあります。お得ですね。
ここでは、皆さんが気になっているであろうマクローリン展開の誤差について考えていきます。
上図はクロソイド曲線について、Excelで数値計算した軌跡とマクローリン近似による軌跡を比較したものです。
重心速度を2000mm/s、微小時間を1msとして計算しています。
高速ターンにおいてスリップ角を考慮しないのは現実的ではありませんが、ここでは誤差の影響が顕著に出るようv=2000mm/sとしました。
この図を見ると見た目には、スラロームに用いる低角度領域ではよく近似できているように見えます。
しかし、図からはどれほどずれているかわかりません。
というわけで、両者の差をグラフにしたものが下図になります。
この図は、
角加速度515rad/ss
重心速度2000mm/s
のパラメータにおいて
「マクローリン近似による推定値」と
「微小時間を1msとして計算した数値計算」を比較したものです。
横軸は機体の角度、縦軸はそれぞれX方向とY方向における差を示しています。
これを見ると180度までの範囲で、ズレは最大でも2mm程度だとわかります。
スラロームとして考えると180度ターンのとき角度が最大なので、クロソイド曲線としては90度までとなります。
そのため、近似によるズレは最大でも1.5mm程度で済みそうです。
皆さんが如何ほどの精度で機体の制御を行っているかはわかりませんが、~2mm程度のズレであれば調整範囲内といってよいのではないでしょうか。
少なくとも私のマウスでは理論値と現実の軌跡とのズレは、これよりはるかに大きいため、調整によって丸めこめると考えています。
最後に重心速度を変えたときズレはどのように変化するかを載せて今回は締めさせていただきます。
式(11)、(13)からも明らかなように速度が大きくなればズレも大きくなります。
PR
Comment
