[PR]
2026年03月12日
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
スラロームによる移動距離近似、その3
2017年04月14日
ようやく3回目です。
まだイントロが終わった段階でしかありませんが。
これまでの記事は1回目の目次からどうぞ。
というわけで数式をいじりながら移動距離を求めていきます。
全部やると長くなりそうなので、今回は円弧部分を求めるところまで。
計算に移る前に以降使う文字の定義を決めておきましょう。
前回の記事からスラロームパラメータとは、「角加速度、目標角度、加速角度、重心速度」だとわかりました。これらをそれぞれ以下のように置くことにします。

また、機体の角度をθと置くことにします(下図参照)。

すると、スラロームの各要素は、それぞれθが以下の範囲内であると表せます。

※ここでは、角減速は角加速と同じように行うとする。つまり、角加速度の絶対値が同じであり、かつ角減速し角速度0になるまでに必要な角度は加速角度θAと等しい。
まず、簡単な円弧部分の移動距離について求めていきます。
スラロームから円弧部分のみを取り出したのが下図になります。

ここで、円弧の曲率半径をRと置きました。
また、移動距離を考えるので、座標軸としてx軸y軸を追加し円の中心をその原点とします。
θAとθT-θAが何故このように決まるのかわからない人は接線をひいて考えることで理解の助けとなるかもしれません。
さて、では円弧の移動距離を考えていきます。

よって、円弧のx軸方向とy軸方向への移動距離をそれぞれ求めることができました。
式(3)、式(4)からパラメータと移動距離の関係を知ることができます。
また、式(3)、式(4)は円弧を決める変数Rと人間が決めるパラメータθTθAによる関数の積の形で移動距離を表すことができています。
よって、将来的には、移動距離とパラメータから曲率半径を求める(円弧の軌跡を求める)ことができそうだと予想されます。
とはいえ、それができるかはクロソイドがどう表されるかによりますが。
というわけで、今回はここまで。
今回わかったことは円弧の移動距離は以下のように表されます。
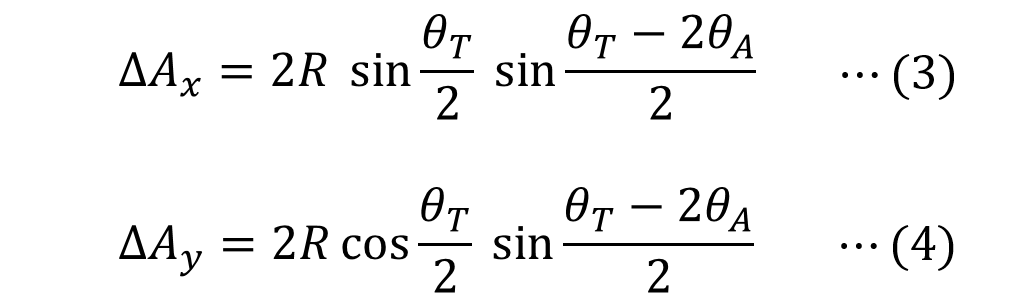
次回はついにクロソイドに入りたいと思います。
まだイントロが終わった段階でしかありませんが。
これまでの記事は1回目の目次からどうぞ。
というわけで数式をいじりながら移動距離を求めていきます。
全部やると長くなりそうなので、今回は円弧部分を求めるところまで。
文字の定義
計算に移る前に以降使う文字の定義を決めておきましょう。
前回の記事からスラロームパラメータとは、「角加速度、目標角度、加速角度、重心速度」だとわかりました。これらをそれぞれ以下のように置くことにします。
また、機体の角度をθと置くことにします(下図参照)。
すると、スラロームの各要素は、それぞれθが以下の範囲内であると表せます。
※ここでは、角減速は角加速と同じように行うとする。つまり、角加速度の絶対値が同じであり、かつ角減速し角速度0になるまでに必要な角度は加速角度θAと等しい。
円弧の移動距離
まず、簡単な円弧部分の移動距離について求めていきます。
スラロームから円弧部分のみを取り出したのが下図になります。
ここで、円弧の曲率半径をRと置きました。
また、移動距離を考えるので、座標軸としてx軸y軸を追加し円の中心をその原点とします。
θAとθT-θAが何故このように決まるのかわからない人は接線をひいて考えることで理解の助けとなるかもしれません。
さて、では円弧の移動距離を考えていきます。
よって、円弧のx軸方向とy軸方向への移動距離をそれぞれ求めることができました。
式(3)、式(4)からパラメータと移動距離の関係を知ることができます。
また、式(3)、式(4)は円弧を決める変数Rと人間が決めるパラメータθTθAによる関数の積の形で移動距離を表すことができています。
よって、将来的には、移動距離とパラメータから曲率半径を求める(円弧の軌跡を求める)ことができそうだと予想されます。
とはいえ、それができるかはクロソイドがどう表されるかによりますが。
まとめ
というわけで、今回はここまで。
今回わかったことは円弧の移動距離は以下のように表されます。
次回はついにクロソイドに入りたいと思います。
PR
Comment
